Activation functions

import torch
import matplotlib.pyplot as plt

Sigmoid function

sigmoid = torch.nn.Sigmoid()
x = torch.arange(-10, 10, step=1)

plt.plot(x, sigmoid(x), 'k-', label = 'sigmoid')
plt.legend()
plt.xlabel('x')
plt.ylabel('f(x)')
plt.show()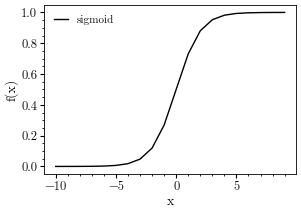

ReLu function

relu = torch.nn.ReLU()
x = torch.arange(-10, 10, step=1)

plt.plot(x, relu(x), 'k-', label = 'ReLu')
plt.legend()
plt.xlabel('x')
plt.ylabel('f(x)')
plt.show()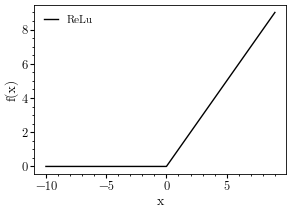

Leaky ReLu

f = torch.nn.LeakyReLU(negative_slope=0.1)
x = torch.arange(-10, 10, step=1.0)

plt.plot(x, f(x), 'k-', label = 'Leaky ReLu')
plt.legend()
plt.xlabel('x')
plt.ylabel('f(x)')
plt.show()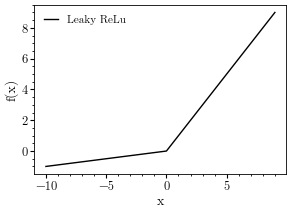

Softmax function

# create a softmax module to apply to the last dimension of the input tensor
f = torch.nn.Softmax(dim=-1)
x = torch.arange(-10, 10, step=1.0)

plt.plot(x, f(x), 'k-', label = 'Softmax')
plt.legend()
plt.xlabel('x')
plt.ylabel('f(x)')
plt.show()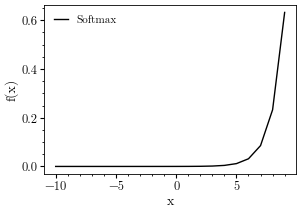

Softmax is useful for a vector input. The sum of the values for each element of the vector becomes 1.0

# create a vector (rank 2 tensor) with 3 elements
x = torch.randn(1, 3)
x

tensor([[-0.4259,  1.3028, -1.4466]])

# apply softmax along the last dim (column)
f = torch.nn.Softmax(dim=1)
y = f(x)
y

tensor([[0.1430, 0.8055, 0.0515]])

# verify the sum of the softmax values
torch.sum(y, dim=1)

tensor([1.])